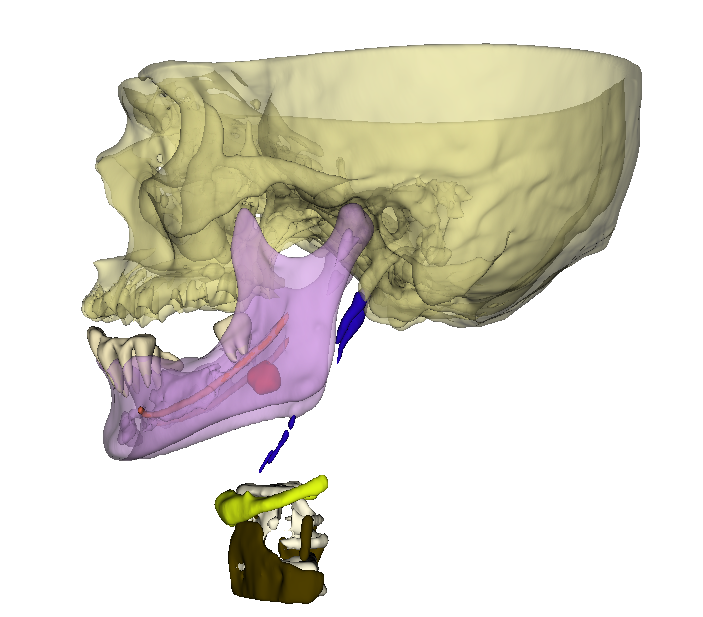
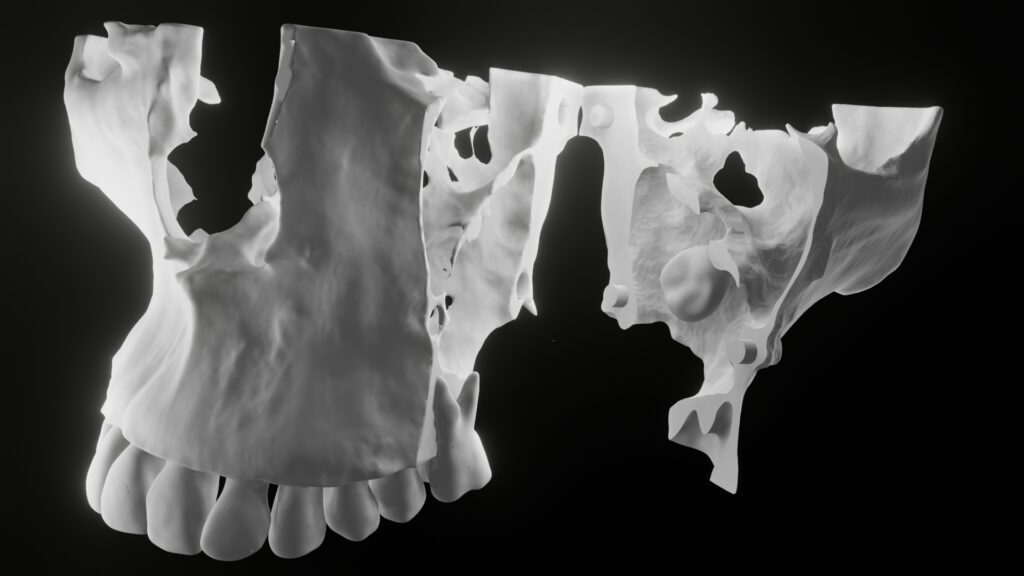
In the world of medical and dental radiology, 3D models have become indispensable tools for visualization, diagnosis, and treatment planning.
To truly grasp the capabilities and limitations of these models, it is essential to understand the fundamentals of 3D geometry—the mathematical and structural principles that form the backbone of 3D representations.
For radiologists and medical professionals entering the world of 3D medical imaging, this overview will help build a solid base for understanding how these complex models are constructed, manipulated, and interpreted.
Points, Vertices, and Coordinates
At the most fundamental level, every 3D model is built from points. Points have no dimension—they represent precise locations in 3D space defined by a set of coordinates. Typically, these coordinates are described in a Cartesian system: (x,y,z)(x,y,z) values that specify position along the three perpendicular axes.
When these points are used as structural elements in 3D models, they are called vertices (singular: vertex). Vertices are the critical building blocks of the model’s shape—they mark where edges meet and define the spatial boundaries of the model.
In medical 3D imaging, vertices correspond to key landmarks or sampled points on anatomical structures reconstructed from imaging data like CT or MRI scans. The accuracy with which vertices represent real anatomical positions directly affects the fidelity of the 3D model.
Edges and Connections
Edges are the straight lines connecting two vertices in 3D space. Together, vertices and edges form the skeleton or wireframe of a 3D model. Each edge defines a direct connection between a pair of points, building the framework upon which surfaces are constructed.
Edges are important in defining the contours and anatomical geometry of the model. In medical contexts, edges help delineate borders of bones, teeth, vessels, or soft tissue features. They also play a key role in how the model can be manipulated—rotated, scaled, or segmented—since edges define the model’s underlying topology.
Effective edges ensure the structural integrity of the 3D mesh and prevent gaps or overlaps that could impair visualization or lead to inaccurate diagnostics.
Faces: Triangles, Quads, and N-gons
Surfaces in 3D are created by connecting multiple edges into polygons / faces. Polygons are flat, two-dimensional shapes embedded in 3D space, composed of a closed sequence of edges and vertices.
The most common polygons used in 3D medical modeling are:
Triangles:
The simplest polygon consisting of three vertices and three edges. Triangles are fundamental because any complex surface can be subdivided into triangles, ensuring the model can be uniformly processed and rendered. Triangular meshes are computationally efficient and widely supported by visualization software.
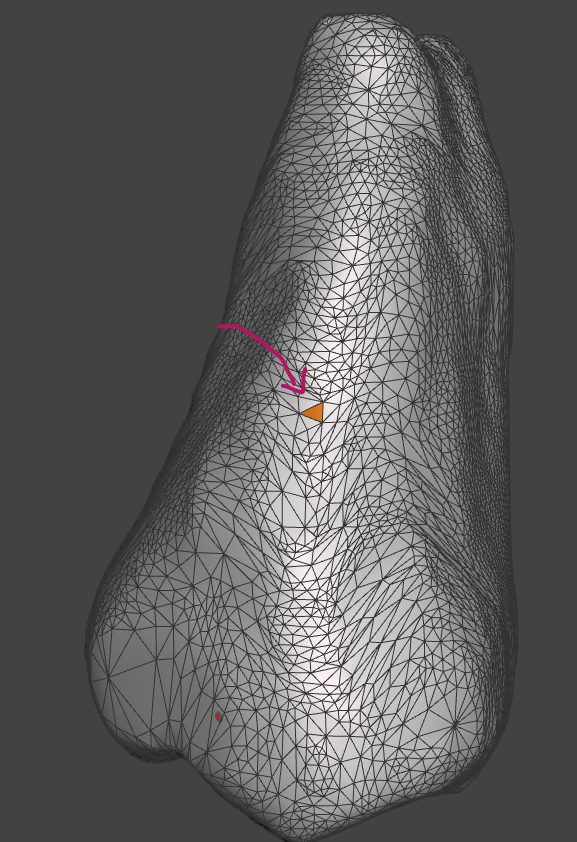
Quads (quadrilaterals):
Polygons with four vertices and four edges. Quads tend to form smoother, more regular surfaces and are often preferred in modeling workflows for their ability to represent organic shapes with less geometric complexity.
Ngons:
Polygons with five or more vertices. While ngons can represent more complex faces, they are less common in medical 3D modeling due to challenges in mesh processing and rendering. Ngons often require further subdivision into triangles or quads for compatibility with most modeling and visualization tools.
Understanding these polygons helps radiologists appreciate how detailed and accurate models are formed, from simple shapes to complex anatomical representations.
Surfaces and Meshes: Definitions and Properties
Surface:
A surface in 3D is a continuous expanse that defines the exterior shape of an object. In medical imaging, surfaces represent the boundaries of anatomical structures like bones, organs, or teeth, derived from segmented imaging data.
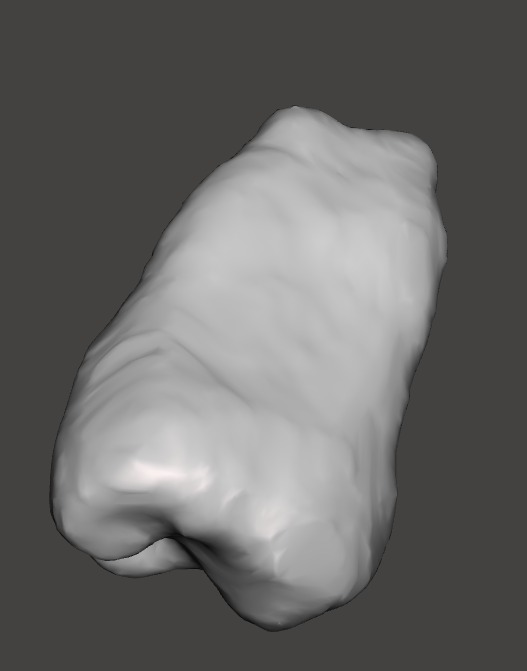
Mesh:
A mesh is a collection of polygons that together approximate a 3D surface. In essence, a mesh is the digital representation of the surface geometry, made up of interconnected vertices, edges, and faces (polygons). Meshes are the most common way to represent 3D anatomical structures in software applications and for 3D printing.
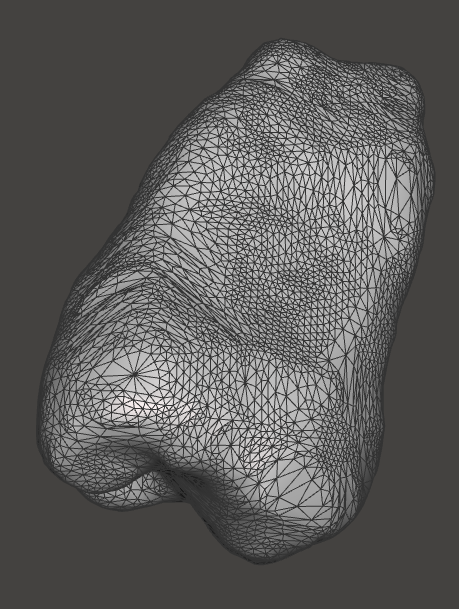
Properties of Meshes Relevant to Medical Imaging:
Resolution: Determined by the number of polygons (usually triangles or quads). Higher resolution models have more detail but require more processing power.
Topology: Describes how vertices, edges, and polygons are connected. Good topology is necessary for realistic deformation (important in surgical simulations) and accurate analysis.
Surface Smoothness and Continuity: Reflects how well the polygons approximate a smooth anatomical surface. Improving this may involve smoothing algorithms without compromising anatomical accuracy.
Manifold vs. Non-manifold Meshes: A manifold mesh is “well-behaved,” meaning it forms a continuous, closed surface without ambiguity. Non-manifold meshes have problematic areas where the mesh doesn’t define a proper volume, possibly causing errors in analysis or 3D printing.
Understanding mesh properties ensures radiologists can interpret the quality and limitations of 3D models, critical when models are used for surgical planning or implantation.
Conclusion
A clear understanding of the fundamentals of 3D geometry—points, vertices, edges, polygons, surfaces, and meshes—is essential for medical and dental radiologists working with advanced 3D models. These concepts not only underpin how anatomical shapes are digitally reconstructed but directly impact clinical applications, from precise diagnosis to customized treatment plans.
With these basics, radiologists can better communicate with modeling specialists, evaluate the accuracy of 3D representations, and confidently integrate 3D technology into their clinical workflow.
With over a decade of experience in dentistry, I specialize in diagnosing a wide range of oral diseases and have developed a deep passion for dental imaging. My interest in CBCT reporting and digital implantology led me to become a pioneer in the concept of diagnostic 3D modelling. Throughout my career, I have supported and educated numerous dentists in mastering CBCT interpretation, virtual implant planning, and the latest advancements in 3D printing for dental applications. Read more about me on the “about me” page.
- Steiner’s Analysis – Free online Cephalometry - November 23, 2025
- A Complete guide to Grayscale values in CT & CBCT - November 15, 2025
- Struggling to get your old PC to run new Radiology software smoothly? Here’s a trick with SSD that might save you. - November 14, 2025
